The notations discussed today are ways to describe behaviors of functions, particularly in the limit, or asymptotic behavior.
The functions need not necessarily be about algorithms, and indeed asymptotic analysis is used for many other applications.
Asymptotic analysis of algorithms requires:
The different asymptotic bounds we use are analogous to equality and inequality relations:
In practice, most of our analyses will be concerned with run time. Analyses may examine:
Our first question about an algorithm's run time is often "how bad can it get?" We want a guarantee that a given algorithm will complete within a reasonable amount of time for typical n expected. This requires an asymptotic upper bound: the "worst case".
Big-O is commonly used for worst case analyses, because it gives an upper bound on growth rate. Its definition in terms of set notation is:
O(g(n)) = {f(n) : ∃ positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) ∀ n ≥ n0}.
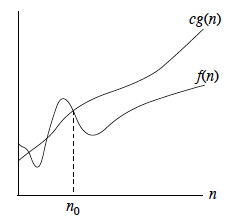
This definition means that as n increases, after a given point n0, f(n) grows no faster than g(n) (as illustrated in the figure): g(n) is an asymptotic upper bound for f(n).
Since O(g(n)) is a set, it would be natural to write f(n) ∈ O(g(n)) for any given f(n) and g(n) meeting the definition above, for example, f ∈ O(n2).
But the algorithms literature has adopted the convention of using = instead of ∈, for example, writing f(n) = O(g(n)). This "abuse of notation" makes some manipulations possible that would be more tedious if done strictly in terms of set notation. (We do not write O(g(n))=f(n); will return to this point).
Using the = notation, we often see definitions of big-O in in terms of truth conditions as follows:
f(n) = O(g(n)) iff ∃ positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) ∀ n ≥ n0.
We assume that all functions involved are asymptotically non-negative. Other authors don't make this assumption, so may use |f(n)| etc. to cover negative values. This assumption is reflected in the condition 0 ≤ f(n).
Show that 2n2 is O(n2).
To do this we need to show that there exists some c and n0 such that (letting 2n2 play the role of f(n) and n2 play the role of g(n) in the definition):
0 ≤ 2n2 ≤ cn2 for all n ≥ n0.
It works with c = 2, since this makes the f and g terms equivalent for all n ≥ n0 = 0. (We'll do a harder example under Θ.)
| These are all O(n2): | These are not: |
|
|
Recall that we did a tedious analysis of the worst case of insertion sort, ending with this formula:
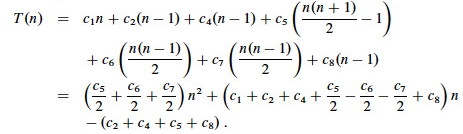
T(n) can be expressed as pn2 + qn - r for suitable p, q, r (p = (c5/2 + c6/2 + c7/2), etc.).
The textbook (page 46) sketches a proof that f(n) = an2 + bn + c is Θ(n2), and we'll see shortly that Θ(n2) → O(n2). This is generalized to all polynomials in Problem 3-1. So, any polynomial with highest order term and (i.e., a polynomial in n of degree d) will be O(nd).
This suggests that the worst case for insertion sort T(n) ∈ O(n2). An upper bound on the worst case is also an upper bound on all other cases, so we have already covered those cases.
Notice that the definition of big-O would also work for g(n) = n3, g(n) = 2n, etc., so we can also say that T(n) (the worst case for insertion sort) is O(n3), O(2n), etc. However, these loose bounds are not very useful! We'll deal with this when we get to Θ (Theta).
We might also want to know what the best we can expect is. In the last lecture we derived this formula for insertion sort:
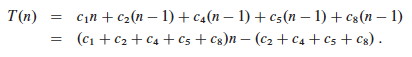
We could prove that this best-case version of T(n) is big-O of something, but that would only tell us that the best case is no worse than that something. What if we want to know what is "as good as it gets": a lower bound below which the algorithm will never be any faster?
We must both pick an appropriate function to measure the property of interest, and pick an appropriate asymptotic class or comparison to match it to. We've done the former with T(n), but what should it be compared to?
It makes more sense to determine the asymptotic lower bound of growth for a function describing the best case run-time. In other words, what's the fastest we can ever expect, in the best case?
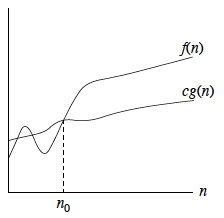
Ω (Omega) provides what we are looking for. Its set and truth condition definitions are simple revisions of those for big-O:
Ω(g(n)) = {f(n) : ∃ positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) ∀ n ≥ n0}.
[The f(n) and cg(n) have swapped places.]
f(n) = Ω(g(n)) iff ∃ positive constants c and n0 such that f(n) ≥ cg(n) ∀ n ≥ n0.
[≤ has been replaced with ≥.]
The semantics of Ω is: as n increases after n0, f(n) grows no slower than g(n) (see illustration).
Sqrt(n) is Ω(lg n) with c=1 and n0=16.
(At n=16 the two functions are equal; try at n=64 to see the growth, or graph it.)
| These are all Ω(n2): | These are not: |
|
|
We can show that insertion will take at least Ω(n) time in the best case (i.e., it won't get any better than this) using the above formula and definition.
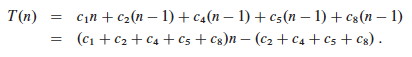
T(n) can be expressed as pn - q for suitable p, q (e.g., q = c2 + c4 + c5 + c8, etc.). (In this case, p and q are positive.) This suggests that T(n) ∈ Ω(n), that is, ∃ c, n0 s.t. pn - q ≥ cn, ∀n ≥ n0. This follows from the generalized proof for polynomials.
We noted that there are loose bounds, such as f(n) = n2 is O(n3), etc., but this is an overly pessimistic assessment. It is more useful to have an asymptotically tight bound on the growth of a function. In terms of algorithms, we would like to be able to say (when it's true) that a given characteristic such as run time grows no better and no worse than a given function. That is, we want to simultaneoulsy bound from above and below. Combining the definitions for O and Ω:
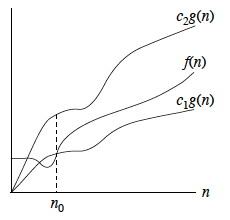
Θ(g(n)) = {f(n) : ∃ positive constants c1, c2, and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n), ∀ n ≥ n0}.
As illustrated, g(n) is an asymptotically tight bound for f(n): after a point, f(n) grows no faster and no slower than g(n).
The book suggests the proof of this theorem as an easy exercise (just combine the two definitions):
f(n) = Θ(g(n)) iff f(n) = Ω(g(n)) ∧ f(n) = O(g(n)).
You may have noticed that some of the functions in the list of examples for big-O are also in the list for Ω. This indicates that the set Θ is not empty.
Reminder: f(n) = Θ(g(n)) iff ∃ positive constants c1, c2, and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n)∀ n ≥ n0.
n2 - 2n is Θ(n2), with c1 = 1/2; c2 = 1, and n0 = 4, since:
n2/2 ≤ n2 - 2n ≤ n2 for n ≥ n0 = 4.
Please try these before you find solutions here.
| These are all Θ(n2): | These are not |
|
|
The O and Ω bounds may or may not be asymptotically tight. The next two notations are for upper bounds that are strictly not asymptotically tight. There is an analogy to inequality relationships:
o(g(n)) = {f(n) : ∀ constants c > 0, ∃ constant n0 > 0 such that 0 ≤ f(n) < cg(n) ∀ n ≥ n0}.
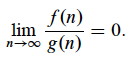
Notice that the quantification is now for all constants c, not that there exists some.
An alternative definition is that f(n) becomes insignificant relative to g(n) as n approaches infinity (see box):
We say that f(n) is asymptotically smaller than g(n) if f(n) = o(g(n))
ω(g(n)) = {f(n) : ∀ constants c > 0, ∃ constant n0 > 0 such that 0 ≤ cg(n) < f(n) ∀ n ≥ n0}.
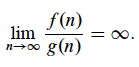
Alternatively, f(n) becomes arbitrarily large relative to g(n) as n approaches infinity (see box):
We say that f(n) is asymptotically larger than g(n) if f(n) = ω(g(n))
The two are related: f(n) ∈ ω(g(n)) iff g(n) ∈ o(f(n)).
We already noted that while asymptotic categories such as Θ(n2) are sets, we usually use "=" instead of "∈" and write (for example) f(n) = Θ(n2) to indicate that f is in this set.
Putting asymptotic notation in equations lets us do shorthand manipulations during analysis.
O(g(x)) on the right hand side stands for some anonymous function in the set O(g(x)).
2n2 + 3n + 1 = 2n2 + Θ(n) means:
2n2 + 3n + 1 = 2n2 + f(n) for some f(n) ∈ Θ(n) (in particular, f(n) = 3n + 1).
The notation is only used on the left hand side when it is also on the right hand side.
Semantics: No matter how the anonymous functions are chosen on the left hand side, there is a way to choose the functions on the right hand side to make the equation valid.
2n2 + Θ(n) = Θ(n2) means for all f(n) ∈ Θ(n), there exists g(n) ∈ Θ(n2) such that
2n2 + f(n) = g(n).
We can do basic algebra such as:
2n2 + 3n + 1 = 2n2 + Θ(n) = Θ(n2)
If we keep in mind the analogy to inequality, many of these make sense, but see the end for a caution concerning this analogy.
Here is where the analogy to numeric (in)equality breaks down: There is no trichotomy. Unlike with constant numbers, we can't assume that one of <, =, > hold. Some functions may be incomparable.
Example: n1 + sin n is incomparable to n since sin n oscillates between -1 and 1, so 1 + sin n oscillates between 0 and 2. (Try graphing it.)
Various classes of functions and their associated notations and identities are reviewed in the end of the chapter: please review the chapter and refer to ICS 241 if needed. Here we highlight some useful facts: