(Can't push more over an edge than its capacity.)
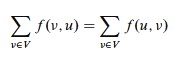
(Flow into a vertex must equal flow out of it, except for the source and sink.)
Many problems involve modeling flow through networks, to maximize flow or look for vulnerabilities. These include liquids flowing through pipes, materials moving through transportation networks, and communication networks.
Flow algorithms also have applications to problems that don't look like flow, such as scheduling.
A flow network is a directed graph G = (V, E) where each edge (u, v) has a capacity c(u, v) ≥ 0, and:
Comments:
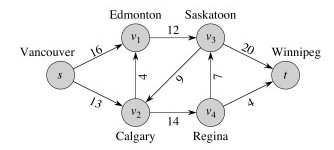
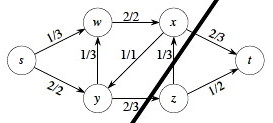
A simple example: the trucking capacity network:
A flow for a network is a function f : V x V → ℜ (that is, f assigns numbers to edges) satisfying:
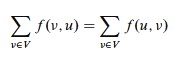
Example with flow/capacity:
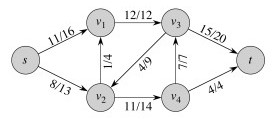
Check flow conservation in this network. Is the in-flow equal to the
out-flow of all internal vertices?
Also, are we making maximum use of the
network to get stuff from s to t? How can we improve it?
The value of flow f = |f| is defined to be the flow out of source minus the flow into the source:
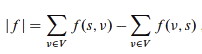
Comments:
What is the value of flow in the example flow network above?
Our formulation disallows anti-parallel edges, exemplified by the edges between v1 and v2 below:
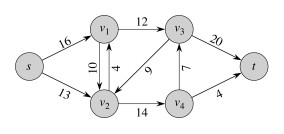
Fortunately they are easy to eliminate. How would you do it? Why not just subtract 4 from 10 to get 6? Click on the image to see an alternate solution.
We also require that there be a single source and sink. We can easily convert networks with multiple sources and sinks by adding a common source s and a common sink t and wiring them in appropriately:
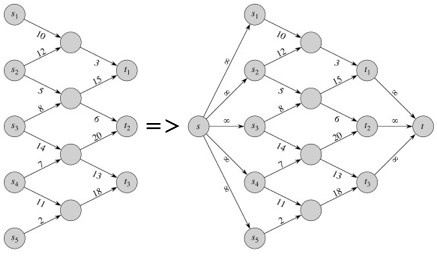
A similar construction can be used to implement a requirement that the source s only has outgoing edges and the sink t only has incoming edges, which simplifies some proofs. (Note that later we introduce residual networks, which necessarily have edges incoming to the source or outgoing from the sink.)
This is the problem we will almost always be solving:
Given G, s, t, and c, find a flow f whose value is maximum.
We take a brief diversion into some relevant graph theory.
A cut (S, T) of a flow network G = (V, E) is a partition of V into S and T = V - S such that s ∈ S and t ∈ T.
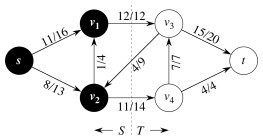
The figure shows an example of a cut, where S = {s, v1, v2} and T = {v3, v4, t}.
The capacity of cut (S, T) is the sum of the capacities of the edges crossing the cut from S to T:
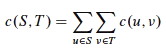
The net flow across cut (S, T) for flow f is the sum of the forward flow minus the backflow:
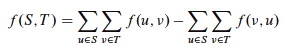
What is the net flow for the cut in this example? The capacity?
Note the assymetry between capacity and net flow of a cut:
Why does this assymetry make sense?
Consider the cut S = {s, w, y}, T = {x, z, t} in the network shown.
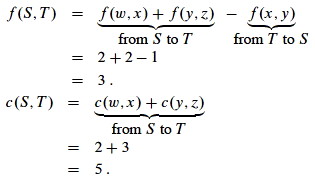
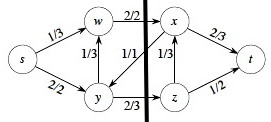
Now consider the cut S = {s, w, x, y}, T = {z, t}.
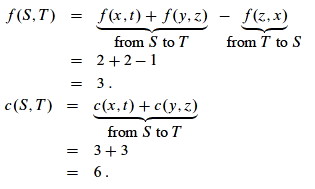
We get the same flow as the previous cut, but higher capacity. It is not an accident that changing cut can change capacity but not flow. Can you explain why?
Definition: a minimum cut of G is a cut whose capacity is minimum over all cuts of G.
The proofs of these are straightforward but involve long manipulations of summations: see CLRS.

For any cut (S, T), f(S, T)
= |f|
(the net flow across any cut equals the value of the
flow).
The intuition is that no matter where you cut the pipes in a network, you'll see the same flow volume coming out of the openings. If you did not, conservation would be violated at some nonempty subset of the vertices.
(This is the answer to the earlier question about why t need not be in the definition of |f|, AND the answer to the question above about why changing the cut can change capacity but not flow.)
The value of any flow ≤ capacity of any cut.
This is again intuitive under the plumbing analogy: if it were false, you could push more flow through the pipes than they can hold.
This is a method, not an algorithm, because there are many ways to do it.


The intuition behind this method is simple: Find a pathway of unused capacity and increase the flow along that pathway. We call this pathway an augmenting path. Repeat until no such pathways are found.
What makes this nontrivial is an apparent paradox: overall flow can sometimes be increased by decreasing flow along certain edges (because they flow in the "wrong" direction or move capacity to a part of the network that can't handle it as well). See whether you can find an example in the graph shown.
Ford Fulkerson manages this by constructing a parallel network of the available or residual capacity. We will return to the method after explaining these concepts.
Given a flow f in a network G = (V, E), consider a pair of vertices u, v ∈ V. How much additional flow can we push directly from u to v? This is the residual capacity cf (u,v):
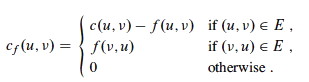
The first case says that if we have not used the full capacity c(u, v) of an edge (u, v) in E then we can increase it by the difference.
The second case says that if we are using f(v, u) of the capacity of (v, u) in E then we have the residual "capacity" of reversing (cancelling) that much flow in the reverse direction (u, v) (notice that the letters are swapped).
Otherwise there is no residual capacity between u and v.
We record these capacities in the residual network Gf = (V, Ef), where
Ef = {(u, v) ∈ V x V : cf (u, v) > 0}.
A residual network is similar to a flow network, except that it may contain antiparallel edges, and there may be incoming edges to the source and/or outgoing edges from the sink. Each edge of the residual network can admit a positive flow.
A flow network is on the left, and its residual network on the right.
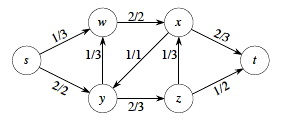
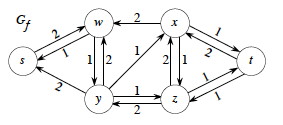
For example, Gf says that we can add two more units from s to w in G or we can take one unit back.
Take a little time to understand the relationship between the two graphs: it's critical, so don't go on until you do!
Every edge (u, v) ∈ Ef corresponds to (u, v) ∈ E or (v, u) ∈ E, and when only part of the capacity of the edge in E is used there may be two corresponding edges in Ef. So, |Ef| ≤ 2 |E| (that is, there can be up to twice as many edges in Ef).
We can define flow f ' in a residual network that satisfies the definition of flow (respecting capacity constraints and flow conservation), but with respect to capacities cf in the network Gf.
Given flows f in G and f ' in Gf, define the augmentation of f by f ', f ↑ f ', to be a function V x V → ℜ:
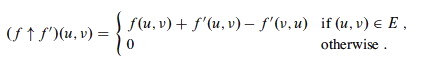
for all u, v∈ V.
In English: To "add" the flow f ' of the residual network Gf to the current flow f in G, for each edge (u, v) in E, increase the flow on (u, v) by f ' (u, v), but decrease it by f ' (v, u) because pushing flow on the reverse edge in the residual network decreases the flow in the original network.

Above we hinted that augmentation is like addition. To do math on flows, this property is very helpful:
Given flow network G, flow f in G, and residual network Gf, let f ' be a flow in Gf. Then f ↑ f ' is a flow in G with value | f ↑ f ' | = | f | + | f ' |.
(A proof with lots of summations in the CLRS book shows that the capacity constraint and flow conservation properties are met, and demonstrates that the value of f ↑ f ' is correct. The proof is easy to follow but more than I want to write here; see CLRS.)
Any simple path p from s to t in Gf is an augmenting path.
Augmenting paths admit more flow along each edge in Gf (because all the edges have positive capacity).
How much more flow can we push from s to t along an augmenting path p? That is, what is the capacity cf (p) of a path? The "weakest link" principle applies:
cf (p)= min{cf (u, v) such that (u, v) is on p}.
Here is a flow network (left) and a residual network (right).


Consider the augmenting path p = ⟨s, w, y, z, x, t⟩ in Gf. The minimum residual capacity of this path is ...what???
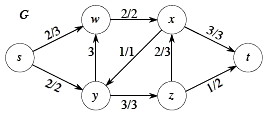
Push that much additional flow along p in G. Notice that the path in Gf goes over G's edge (y, w) in the reverse direction, so we subtract that much flow from the edge in G.
As a result, edge (y, w) has f(y, w) = 0, so we omit the flow, showing only c(y, w) = 3 in the revised G to the left.
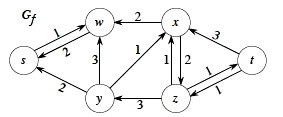
Now let's update the residual network Gf.
Make sure you understand how we got the graph to the right before going on.
Summarizing the Process: Always search for augmenting paths in Gf and use them to reweight flows in G, which then leads to constructing a new Gf.
On every exam the last several years half the students got this wrong, doing in one graph what they should do in the other . Study it again!
Is there an augmenting path in the second Gf above? How can we tell?
Notice that no edges cross the cut ({s, w}, {x, y, z, t}) in the forward direction in Gf, so no path can get from s to t.
Since no further augmentation is possible, we claim that the flow shown in G is a maximal flow. This theorem tells us we are right.
The following are equivalent (see text for lemma, corollary and proof):
This means that if (2) we can't find augmenting paths or (3) have achieved a flow equivalent to the capacity of some cut, then we are done: (1) we have found the maximum flow.
(3) also lets us predict what the max flow will be: it will be equal to the capacity of the minimum cut (as measured by capacity). Hence "max flow (is) min cut".
This is the central theorem of today's topic: make sure you understand it.
Now we take the Ford Fulkerson method and make it into an algorithm based on this intuition: keep augmenting flow along an augmenting path until there is no augmenting path. The flow attribute is represented using dot notation on edges: (u, v) . f is the flow over edge (u, v).
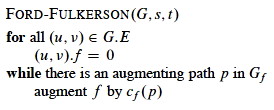
or in more detail
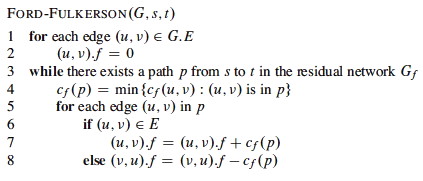
(Line 4 finds the "weakest link" on the augmenting path. Line 7 adds flow. Line 8 reduces flow.)
Runtime depends the method used to find paths, and on what kinds of values capacities c can be. It's best to use integer capacities when possible: we'll see why below.
The initialization lines 1-2 is O(E).
The cost to find a path p from s to t in line 3 depends on the method used. Breadth-First-Search or Depth-First-Search will work, and these are O(V + E). This is a connected graph, so |E| ≥ |V| − 1, so this reduces to O(E).
The rest of the work in the while loop is of lower complexity, so the work of each pass of the while loop is O(E).
How many times will the while loop run? For integer costs:
When capacities are integers and f* is small, this is a fast algorithm. If capacities are not integers, it is possible for each iteration to increase flow by an arbitrarily small amount, and we cannot bound the number of iterations without further information. (If capacities are irrational numbers, Ford-Fulkerson might never terminate!)
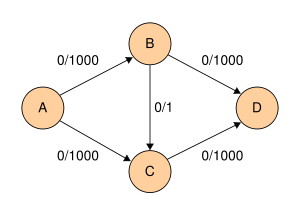
The example to the right illustrates the classic worst case scenario when f* is large. One could:
... requiring 2000 iterations due to the unlucky choice of augmenting paths.
Edmonds-Karp come to the rescue with an insight that controls the order in which Ford-Fulkerson explores paths.
Notice that in the example above, if the shortest paths (by number of edges, not considering weight) are considered first, then the anomaly does not occur. We would find augmenting path ⟨(A,B), (B,D)⟩ to increase flow by 1000, then finish the job with augmenting path ⟨(A,C), (C,D)⟩, or find the second and then the first.
Edmonds-Karp is the Ford-Fulkerson algorithm but with the constraint that augmenting paths are computed by Breadth-First Search of Gf. ( I told you that those search algorithms are widely useful!)
A proof in the CLRS text shows that the number of flow augmentations performed by Edmunds-Karp is O(VE). Since each BFS is still O(E) in a connected graph, Edunds-Karp runs in O(V E2) time. (This is O(V3) in sparse graphs and O(V5)in dense graphs.) The proof in CLRS works by bounding distances to vertices in Gf.
Even better bounds are possible: this has been a very active area of algorithm development. Sections 26.4-26.5 of CLRS describe push-relabel algorithms that are as fast as O(V3) on any flow network. The notes at the end of the chapter discuss faster algorithms.
There are many variations of Maximum Flow, such as including multiple sources and sinks; including costs and trying to minimize cost; including different kinds of material that take different capacities to transport; etc. Some can be very difficult to solve.
Maximum Flow can also be used to solve problems that don't look like flow problems. Here is an example.
Suppose we want to maximize ...
... etc. We make a bipartite graph G = (V, E) where V = L ∪ R such that all edges go between L and R, and edges in E indicate compatible entities.
A matching is a subset of the edges M ⊆ E such that for all v ∈ V, zero or one edges of M are incident on v. (0: v is unmatched; 1: v is matched; > 1 is not allowed.) Here is one example with two solutions:
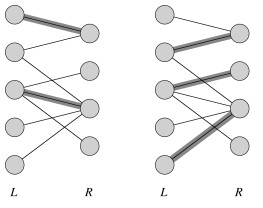
On the left we can see a nonmaximal matching, and on the right a maximum matching, or matching of maximum cardinality: |M| ≥ |M'| ∀ matchings M'.
Given G, define flow network G' = (V', E'):
Then just run Ford-Fulkerson (Edumunds-Karp is not required, as all edges have unit value):
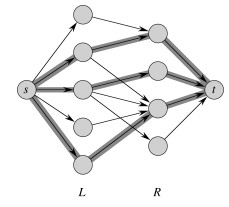
This works because a maximum flow must use the maximum number of (unitary capacity) edges across the cut (L, R).
Previously we established that Ford-Fulkerson is O(E f*).
In the present problem we are running Ford-Fulkerson on E', but E' = O(E) since we are adding no more than V edges (to vertices in L and vertices in R). Also, the flow value f* = O(V) since edges are of unit value and you can't have flow across more edges than there are in min(|L|, |R|) = O(V).
Therefore, bipartite matching can be computed with Ford-Fulkerson in O(VE).
We have just seen an example of problem reduction: reducing the maximum bipartite matching problem to a flow problem and using a flow algorithm to solve it. Last week we saw another problem reduction: solving job scheduling by modeling it as a shortest-paths problem.
Problem reduction is a common theme in computer science. In Topic 21, we will see how the flow problem reduces to the linear programming problem. In later topics, we'll consider reduction of classes of problems known as "P" and "NP", and encounter the greatest unsolved problem in computer science.