x1 + 3x2 − 4x3 = 8
x1 + x2 − 2x3 = 2
−x1 − 2x2 + 5x3 = −1
If you have a background in Gaussian Elimination and read and understand Sections 29.0-29.3 of CLRS, up through the description of Simplex (you need not read the proofs that follow), these objectives will be met. (The material of CLRS Sections 29.4-29.5 is excellent, but we don't need to see all the proofs concerning Simplex to use it.)
If you don't have a background in Gaussian Elimination, then reading and understanding Section 28.1 of CLRS would provide it. However, Section 28.1 provides more detail than is needed to get the gist of Gaussian Elimination and the Simplex. I found Sedgewick's (1984), Chapter 5 presentation of Gaussian Elimination to be clear and sufficient. I also found his presentation of Linear Programming in Chapter 38 useful for its clear narrative around an example.
For a full study of linear programming I recommend this reading sequence:
If you don't have time for the full reading:
No Screencasts were made for this topic.
The following brief conceptual overview of Linear Programming and its roots in Gaussian Elimination is based largely on Chapters 5 and 38 of: Robert Sedgewick (1983). Algorithms. Reading, MA: Addison-Wesley. First Edition (available on Internet), with some comments from CLRS Chapter 29.
Mathematical programming is the process of modeling a problem as a set of mathematical equations. (The "programming" is in mathematics, not computer code.)
Linear programming is mathematical programming where the equations are linear equations in a set of variables that model a problem, and include:
A large and diverse set of problems can be expressed as linear programs and solved. Examples include:
We begin with examples of problems for which we already have more efficient algorithms. The point of revisiting them here with less efficient linear programming solutions is to show you how linear programming works in terms of familiar problems; and also to reinforce the recurring theme that problems can be solved with different algorithms if you change problem representation.
The Bellman-Ford algorithm for single-source shortest paths uses the Relax procedure to find a distance v.d, where for every edge (u, v) ∈ E, v.d ≤ u.d + w(u, v) (since Relax changes v.d precisely when this is not true). Also, s.d for the source vertex s is always 0.
We can translate these observations directly into a linear program for the single-pair shortest-path problem from s to t. We will use notation dv instead of v.d to be consistent with typical linear programming notation:
Maximize: dt
Subject to:
dv ≤ du+ w(u, v), ∀ (u, v) ∈ E
s.d = 0.
The expression dv ≤ du+ w(u, v) is a constraint based on what Relax guarantees, and s.d = 0 by definition (assuming no negative weight cycles).
But why are we maximizing dt when we seek shortest paths?
(Compare to the fact that we needed to find longest paths when determining the shortest time in which a set of jobs could finish in the parallel scheduling problem given in class.)
The extension to single-source all-destinations is straightforward: maximize the sum of the destination distances.
The custom algorithms for single-source and indeed all-pairs shortest paths will be more efficient than solving these problems with linear programming, but it is very easy to write these linear programs, and this example (and the next) illustrates how linear programming works in terms of a familiar example.
Next we show how to model a max-flow problem with linear programming. Instead of writing f(s,a) to indicate the flow over edge (s,a) (for example), we follow the conventions of the linear programming literature and write fsa. (Sedgewick uses XAB.) CLRS present a more general template for any flow network, whereas here we look at a specific example:
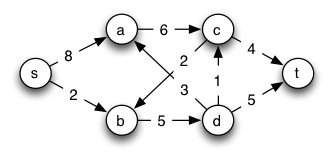
Maximize: fsa+ fsb
Subject to:
fsa ≤ 8 fsb ≤ 2
fac ≤ 6 fda ≤ 3
fbd≤ 5 fcb ≤ 2
fct ≤ 4 fdt ≤ 5
fsa + fda = fac fsb + fcb = fbd
fdt + fda + fdc = fbd fcb + fct = fac
fsa, fsb, fac, fcb, fct, fbd, fda, fdt ≥ 0.
The expression to be maximized,
fsa + fsb
is the flow over the edges coming out of the source, and hence will be the flow of the entire network. If the linear program maximizes this, then we have found the max flow. (If there are edges incoming to s we can subtract these in the expression to be maximized.)
These inequalities capture edge capacities:
fsa ≤ 8; fsb ≤ 2; fac ≤ 6; fda ≤ 3; fbd ≤ 5; fcb ≤ 2; fct ≤ 4; fdt ≤ 5.
These equalities capture the conservation of flow at vertices (I've reordered the last two to show that it's flow in = flow out):
fsa + fda = fac (flow through a)
fsb + fcb = fbd (flow through b)
fac = fcb + fct (flow through c)
fbd = fdt + fda (flow through d)
The final eight inequalities (written in one line for brevity) express the constraint that all flows must be positive:
fsa, fsb, fac, fcb, fct, fbd, fda, fdt ≥ 0.
The Simplex algorithm (discussed later and in the readings), when given a suitable form of these equations (see section 29.1 CLRS), will return an assignment of values to variables fsa, ... fdt that maximizes the expression fsa + fsb and hence flow.
The Edmonds-Karp flow algorithm is more efficient than the Simplex algorithm for solving this version of the max-flow problem. However, Edmonds-Karp is difficult to modify for problem variations such as multiple commodities or dealing with cost-benefit tradeoffs. These additional constraints are easy to add to a linear program.
In general, if a problem can be expressed as a linear program it may be quicker from a development standpoint to do that rather than to invent a custom algorithm for it. Linear programming covers a large variety of problems.
The point here is to introduce linear programming with a familiar example, and to illustrate its generality, but this also provides another example of "problem reduction", a concept that will be at the core of the final topic of this course on Complexity Theory & NP-Completeness.
The Simplex algorithm works in a manner similar to (derived from) Gaussian Elimination for solving a set of linear equations.
Invented by Chinese mathematicians a few thousand years ago, and in Europe by Newton and revised by Gauss, Gaussian elimination is a two part method for solving a system of linear equations.
As a simple example, suppose we have the following system:
x + 3y − 4z = 8
x + y − 2z = 2
−x − 2y + 5z = −1
The goal is to find values of x, y, and z that satisfy these equations. (Recall that there may be zero, one, or an infinite number of solutions, and you need as many equations as variables to have a unique solution.)
If we think of the variables as subscripted as shown on the left, then we can rewrite the system of equations as a matrix equation using the subscripts as column indices as shown on the right:
x1 + 3x2 − 4x3 = 8 |
|
|---|
The following operations can be done on systems of linear equations such as the above. (Later, in the section on linear programing, we'll drop the parentheses and put everything in one matrix. Then, the operations below will be operations on rows and columns of the matrix.)
Gaussian elimination is a systematic way of applying these operations to make the value of one variable obvious (forward elimination), and then substituting this value back into the other equations to expose their values (backward substitution).
Forward elimination turns the matrix into a triangular matrix, where there is only one variable in the last equation, only that variable plus one more in the next equation up, etc.
For example, replace the second equation by the difference between the first two:
Before: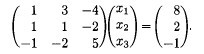
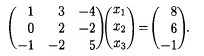
One term has gone to 0: this means x1 has been eliminated from the second equation. Let's eliminate x1 from the third equation by replacing the third by the sum of the first and the third:
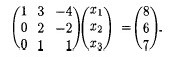
Now if we replace the third equation by the difference between the second and twice the third, we can eliminate x2 from the third row, leaving a triangular matrix. Writing the result as equations:
x1 + 3x2 − 4x3 = 8
2x2 − 2x3 = 6
−4x3 = −8
At the completion of the forward elimination phase, the equations are easy to solve.
It is easy to determine from the third equation that x3 = 2. Substituting that into the second equation, we can derive x2:
2x2 − 4 = 6
x2 = 5
Substituting this and x3 = 2 into the equation above (rewritten below) solves for x1:
x1 + 3x2 − 4x3 = 8
x1 + 15 − 8 = 8
x1 = 1
In general we can solve systems of linear equations as written on the left by converting them into matrices as written on the right:
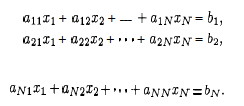
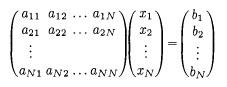
or Ax = b in matrix equation form. It is convenient to represent this entire system in one N x (N+1) matrix consisting of A and the last column for b:
a11 a12 ... a1N b1
a21 a22 ... a2N b2
...
aN1 aN2 ... aNN bN
We can eliminate
In general, the algorithm for forward elimination eliminates the ith variable in the jth equation by multiplying the ith equation by aji / aii and subtracting it from the jth equation, for i+1 ≤ j ≤ N.
We use aji / aii because (aji / aii) * aii = aji, so when we subtract row i from row j we get aji - aji = 0 in cell j,i.
The essential idea can be expressed in this pseudocode fragment (translated from Sedgewick's Pascal):
for i = 1 to N do
for j = i + 1 to N do
for k = N + 1 downto i do
a[j,k] = a[j,k] − a[i,k] * a[j,i] / a[i,i]
There are three nested loops. Trivial Question: How do the loops grow with N? What's the complexity?
This code is too simple: In an actual implementation, various issues must be dealt with, including:
The process of elimination is also called pivoting, a concept that shows up in the application to linear programming.
Sedgewick presents an improved version as a Pascal procedure. If you want to understand the algorithm at this level of detail you should read CLRS 28.1.
Linear programs are systems of linear equations, but with the additional twists that
These two are related:
In fact, these points capture our motivations, in many cases, for using linear programming for real-world problems! There are many ways to act (i.e., many solutions), but we want to know which one is the best (i.e., maximized objective function). The constraints model a set of possible solutions, and the objective function helps us pick one that maximizes something we care about. Linear programming is a general way to approach any such situation that can be modeled with linear equations.
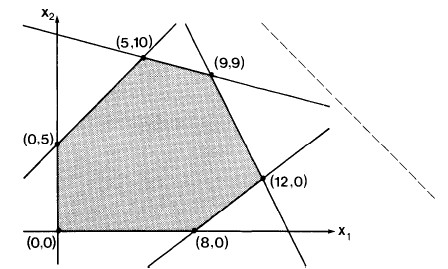
For example, a simple linear program in two variables might look like this:
−x1 + x2 ≤ 5
x1 + 4x2 ≤ 45
2x1 + x2 ≤ 27
3x1 − 4x2 ≤ 24
x1, x2 ≥ 0
We can graph this example as shown:
Each inequality divides the plane into one half in which a solution cannot lie and one in which it can.
For example, x1 ≥ 0 excludes solutions to the left of the x2 axis, and −x1 + x2 ≤ 5 means solutions must lie below and to the right of the line −x1 + x2 = 5, shown between (0,5) and (5,10).
Solutions must lie within the feasible region defined by the intersection of the regions defined by the constraint equations. That region is called the simplex. In the above example, each equation defines a half plane and the simplex, shaded grey in the above figure, is the intersection of these half planes. In systems with more variables the regions are in higher dimensions that are harder to visualize.
The simplex is a convex region: for any two points in the region, all points on a line segment between them are also in the region. Convexness can be used to show an important fact:
The objective function is always maximized at one of the vertices of the simplex.
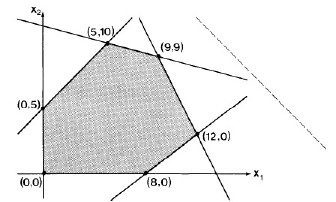
Think of the objective function (here, x1 + x2, the dotted line) as a line of known slope but unknown position. Imagine the line being slid towards the simplex from infinity. If there is a solution, it will first touch the simplex at one of the vertices (one solution) or coincide with an edge (many solutions) that includes a vertex.
Where would this line touch the simplex?
The algorithm does not actually slide a line. Rather, this geometric interpretation tells us that the algorithm need only need search for a solution at the vertices of the convex simplex.
The simplex method systematically searches the vertices, moving to new vertices on which the objective function is no less, and is usually greater than the value for the previous vertex. An example will be given below. See CLRS 29.3 for details of the algorithm.
The geometric interpretation extends to more variables = dimensions.
In three dimensions,
In n dimensions,
The anomalous situations get much harder to detect in advance as dimensions increase, so it is important to handle them well in the code.
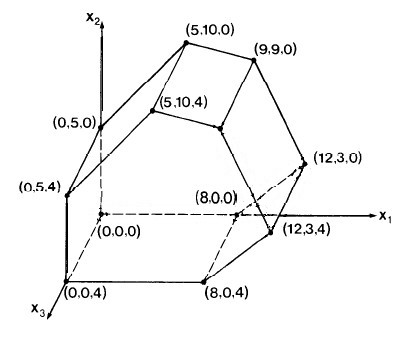
As an example, add the inequalities x3 ≤ 4 and x3 ≥ 0 to our previous example. The simplex becomes a 3-D solid:
−x1 + x2 ≤ 5
x1 + 4x2 ≤ 45
2x1 + x2 ≤ 27
3x1 − 4x2 ≤ 24
x3 ≤ 4
x1, x2, x3 ≥ 0
If the objective function is defined to be x1 + x2 + x3, this is a plane perpendicular to the line x1= x2 = x3. Imagine this plane being brought from infinity to the origin: where would it hit the simplex?
Again, the algorithm we discuss below does not actually move planes from infinity; this is just a way of visualizing the fact that an optimal solution must lie on some vertex of the n-dimensional simplex, so we need only search these vertices.
Now we see how pivoting from Gaussian elimination is used. Pivoting is analogous to moving between the vertices of the simplex, starting at the origin. First, we need to prepare the data ...
(Note: Sedgewick does not distinguish between standard and slack forms; this discussion is based on CLRS section 29.1, to which the reader is referred for details.)
When equations are written to model a problem in a natural way, they may have various features that are not suitable for input to the Simplex Method. We begin by conversion into standard form:
Given n real numbers c1, c2, ... cn (coefficients on objective function), m real numbers b1, b2, ... bm (constants on right hand side of equations),
and mn real numbers aij for i = 1, 2 ... m and j = 1, 2, ... n (coefficients on variables in equations),
find real numbers x1, x2, ... xn (the variables)that maximize: Σj=1,n cj xj (the objective function)
subject to: Σj=1,n aij xj ≤ bj for i = 1, 2, ... m (regular constraints)
and xj ≥ 0, for j = 1, 2, ... n (nonnegativity constraints)
The following conversions may be needed to convert a linear program into standard form (see CLRS for details and justification):
Our example above is already in standard form, except that some of the coefficients aij are equal to 1 and are not written out, and we have not written terms with 0 coefficents. Making all aij explicit, we would write:
−1x1 + 1x2 + 0x3 ≤ 5
1x1 + 4x2 + 0x3 ≤ 45
2x1 + 1x2 + 0x3 ≤ 27
3x1 − 4x2 + 0x3 ≤ 24
0x1 + 0x2 + 1x3 ≤ 4
x1, x2, x3 ≥ 0
The Simplex Method is based on methods (akin to Gaussian elimination) for solving systems of linear equations that require that we work with equalities rather than inequalities (except for the constraints that the variables are non-negative).
We can convert standard form into slack form by introducing slack variables, one for each inequality, that "take up the slack" allowed by the inequality. (These will be allowed to range as needed to do so.)
For example, instead of x1+ 4x2 ≤ 45, we can write x1 + 4x2 + y = 45, where y can range over the values needed to "take up the slack" between inequality and equality.
Applying this idea to the 3-D example above, and using a different yi for each equation, we can model that example with:
Maximize x1 + x2 + x3 subject to the constraints:−1x1 + 1x2 + 0x3 + y1 = 5
1x1 + 4x2 + 0x3 + y2 = 45
2x1 + 1x2 + 0x3 + y3 = 27
3x1 − 4x2 + 0x3 + y4 = 24
0x1 + 0x2 + 1x3 + y5 = 4
x1, x2, x3, y1, y2, y3, y4, y5 ≥ 0
There are m equations in n variables, including up to m slack variables (one for each inequality). (Note: in using n and m, I am following CLRS. Sedgewick uses M for number of variables and N for number of equations.)
We can now write the slack-form system of equations (e.g., above) as a matrix (e.g., shown below), where the 0th row contains the negated coefficients of the objective function. Sedgewick describes how this negation directs the procedure to select the correct rows and columns for pivoting), and the (n+1)th column has the numbers on the right hand side of the equation.

We want to perform pivot operations, using the same row and column manipulations as for Gaussian elimination.
As we proceed, the upper right cell will have the current value of the objective function. We always want to increase this. The question is what strategy to take.
The most popular strategy is greatest increment:
An alternative strategy is steepest descent (actually ascent!): evaluate the alternatives and choose the column that increases the objective function the most.
We'll solve the example given above and copied below. Keep in mind that row indices start at 0, but column indices start at 1. (See Sedgewick for discussion of issues concerning staying in the simplex, detecting unbounded simplexes, and avoiding circularity; and then CLRS if you want details and proofs.)

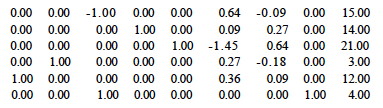
There are three columns with the smallest value (-1) in row 0; we choose to operate on the lowest indexed column 1. Dividing the last number by the positive values in this column, 45/1 = 45 (row 2), 27/2 = 13.5 (row 3) and 24/3 = 8 (row 4), so we choose to pivot on row 4, as this has the smallest result.
Pivot for row p= 4 and column q = 1 by adding an appropriate multiple of the fourth row to each of the other rows to make the first column 0 except for a 1 in row 4):

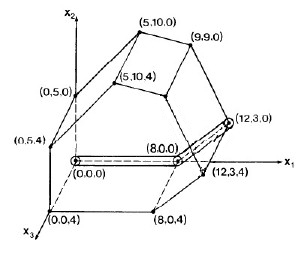
After that pivot, only x1 is a basis variable. Setting the others to 0, we have moved to vertex (8,0,0) on the simplex (see figure), and the objective function has value 8.00 (upper right corner of matrix above).
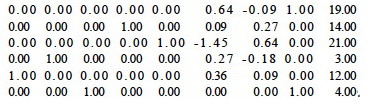
Now, column 2 has the smallest value. Rows 2 and 3 are candidates: for row 2, 37/5.33 = 6.94; and for row 3, 11/3.67 = 2.99. We choose row 3. Pivoting on row p = 3 and column q = 2:
After that pivot, x1 and x2 are basis variables, with values 12 and 3 respectively, so we are at vertex (12,3,0). The objecive function has value 15.00. The figure to the right shows how we are moving through the space.
Now pivot on column q = 3 (it has -1 in row 0) and row p = 5 (it has the only positive value in column 3).
Now all three xi are in the basis, and we are at vertex (12,3,4).
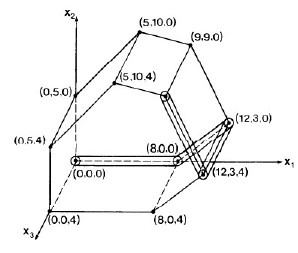
But we are not done: there is still a negative value in row 0 (at column 7), so we know that we can still increase the objective function. I leave it to you to do the math to verify that row 2 will be selected. Pivoting on row p = 2 and column q = 7, we get::
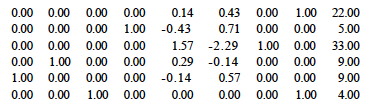
Now row 0 has no negative values, and the columns for the three variables of interest are in the basis (all 0 except one 1 in each). We can read off the solution: x1 = 9, x2 = 9, and x3 = 4, with optimum value 22.
(Here I briefly explain Sedgewick's Pascal code, but if you want to understand the algorithm in detail I recommend going to CLRS for a more current treatment in pseudocode you are familiar with.)
Keep in mind that for Sedgewick there are N equations in M variables.
The main procedure finds values of p and q and calls pivot, repeating until the optimum is reached (q=M+1) or the simplex is found to be unbounded (p=N+1).
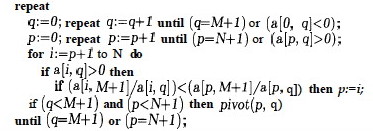
The pivot procedure has similarities to Gaussian elimination. (The for loops below correspond to the two innermost for loops of Gaussian elimination, and the outer for loop of Gauss corresponds to the repeat loop in the main procedure above):
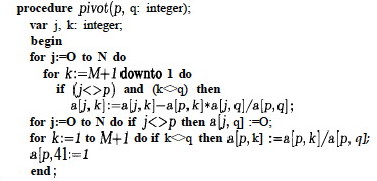
The innermost line is where one row is scaled and subtracted from another. Other details are discussed in Sedgewick's chapter, including the need to implement cycle avoidance and test whether the matrix has a feasible basis (absent from the code above).
At this point, I highy recommend reading CLRS Sections 29.0 (the introduction to the chapter) through the middle of 29.3 (where the Simplex algorithm is introduced: as a "consumer" of the algorithm you don't need to read the proofs that follow in the rest of the section).