The video lectures and notes below provide material not found in the textbook: defining graphs, an ADT, and implementations.
The following material is essential to understand the material of subsequent weeks of this course, and should be well understood.
A graph G is a pair
G = (V, E)
where
V = {v1, v2, ... vn}, a set of vertices
E = {e1, e2, ... em} ⊆ V ⊗ V, a set of edges.
In an undirected graph the edge set E consists of unordered pairs of vertices. That is, they are sets e = {u, v}. Edges can be written with this notation when clarity is desired, but we will often use parentheses (u, v).
In most applications, self loops are not allowed in undirected graphs. That is, we cannot have (v, v), which would not make as much sense in the set notation {v, v}.
We say that e = {u, v} is incident on u and v, and that the vertices u and v are adjacent. The degree of a vertex is the number of edges incident on it.
The handshaking lemma is often useful in proofs:
Σv∈Vdegree(v) = 2|E|
(It takes two hands to shake: Each edge contributes two to the sum of degrees.)
In a directed graph or digraph the edges are ordered pairs (u, v). Directed edges are sometimes called arcs.
We say that e = (u, v) is incident from or leaves u and is incident to or enters v. The in-degree of a vertex is the number of edges incident to it, and the out-degree of a vertex is the number of edges incident from it.
Self loops (v, v) are generally allowed in directed graphs (though they may be excluded by some algorithms or for applications where they do not make sense).
In the social network analysis literature, vertices are often called nodes and edges are often called ties.
A path of length k is a sequence of vertices ⟨v0, v1, v2, ... vk⟩ where (vi-1, vi) ∈ E, for i = 1, 2, ... k. (Some authors call this a "walk".) The path is said to contain the vertices and edges just defined.
A simple path is a path in which all vertices are distinct. (The "walk" authors call this a "path").
If a path exists from u to v we say that v is reachable from u.
In an undirected graph, a path ⟨v0, v1, v2, ... vk⟩ forms a cycle if v0 = vk and k ≥ 3 (as no self-loops are allowed).
In a directed graph, a path forms a cycle if v0 = vk and the path contains at least one edge. (This is clearer than saying that the path contains at least two vertices, as self-loops are possible in directed graphs.) The cycle is simple if v1, v2, ... vk are distinct (i.e., all but the designated start and end v0 = vk are distinct). A directed graph with no self-loops is also simple.
A graph of either type with no cycles is acyclic. A directed acyclic graph is often called a DAG.
A graph G' = (V', E') is a subgraph of G = (V, E) if V' ⊆ V and E' ⊆ E.
An undirected graph is connected if every vertex is reachable from all other vertices. In any connected undirected graph, |E| ≥ |V| - 1 (see also discussion of tree properties). The connected components of G are the maximal subgraphs G1 ... Gk where every vertex in a given subgraph is reachable from every other vertex in that subgraph, but not reachable from any vertex in a different subgraph.
A directed graph is strongly connected if every vertex is reachable from all other vertices while respecting the direction of the edges (arcs). The strongly connected components are the subgraphs defined as above. A directed graph is thus strongly connected if it has only one strongly connected component. A directed graph is weakly connected if the underlying undirected graph (converting all tuples (u, v) ∈ E into sets {u, v} and removing self-loops) is connected.
A bipartite graph is one in which V can be partitioned into two sets V1 and V2 such that every edge connects a vertex in V1 to one in V2. Equivalently, there are no odd-length cycles.
A complete graph is an undirected graph in which every pair of vertices is adjacent.
A weighted graph has numerical weights associated with the edges. (The allowable values depend on the application. Weights are often used to represent distance, cost or capacity in networks.)
Asymptotic analysis is often in terms of both |V| and |E|. Within asymptotic notation we leave out the "|" for simplicity, for example, writing O(V + E), O(V2 lg E), etc. instead of O(|V| + |E|), O(|V|2 lg |E|), etc.
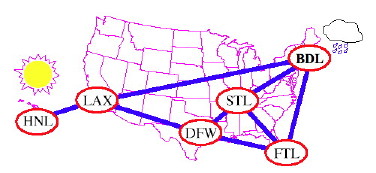
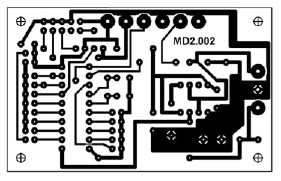
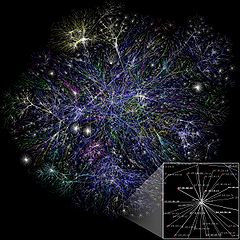
Here we see graphs (clockwise from upper left) for airline flight routes, electrical circuits, the high level struture of the Internet, and a social network (authors who publish together). Take ICS 422 Network Science Methodology if you want to learn more!

This is a typical set of operations for the Graph Abstract Data Type. Further detail is in the Goodrich & Tamassia excerpt uploaded to Laulima. (When we had programming assignments, students were required to implement all of these!)
numVertices() Returns the number of vertices |V|
numEdges() Returns the number of edges |E|
vertices() Returns an iterator over the vertices V
edges() Returns an iterator over the edges E
degree(v)
Returns the number of edges (directed and undirected) incident on v.
adjacentVertices(v) Returns an iterator of the vertices adjacent to v.
incidentEdges(v) Returns an iterator of the edges incident on v.
endVertices(e) Returns an array of the two end vertices of e.
opposite(v,e)
Given v is an endpoint of e.
Returns the end vertex of e different from v.
Throws InvalidEdgeException when v is not an endpoint of e.
areAdjacent(v1,v2) Returns true iff v1 and v2 are adjacent by a single edge.
directedEdges() Returns an iterator over the directed edges of G.
undirectedEdges() Returns an iterator over the undirected edges of G.
inDegree(v) Returns the number of directed edges (arcs) incoming to v.
outDegree(v)
Returns the number of directed edges (arcs) outgoing from v.
inAdjacentVertices(v) Returns an iterator over the vertices adjacent to v by incoming edges.
outAdjacentVertices(v) Returns an iterator over the vertices adjacent to v by outgoing edges.
inIncidentEdges(v) Returns an iterator over the incoming edges of v.
outIncidentEdges(v) Returns an iterator over the outgoing edges of v.
destination(e)
Returns the destination vertex of e, if e is directed.
Throws InvalidEdgeException when e is undirected.
origin(e)
Returns the origin vertex of e, if e is directed.
Throws InvalidEdgeException when e is undirected.
isDirected(e) Returns true if e is directed, false otherwise
insertEdge(u,v)
insertEdge(u,v,o)
Inserts a new undirected edge between two existing vertices, optionally containing
object o.
Returns the new edge.
insertVertex()
insertVertex(o)
Inserts a new isolated vertex optionally containing an object o (e.g., the
label associated with the vertex).
Returns the new vertex.
insertDirectedEdge(u,v)
insertDirectedEdge(u,v,o)
Inserts a new directed edge from an existing vertex to another.
Returns the new edge.
removeVertex(v)
Deletes a vertex and all its incident edges.
Returns object formerly stored at v.
removeEdge(e)
Removes an edge.
Returns the object formerly stored at e.
Methods for annotating vertices and edges with arbitrary data.
setAnnotation(Object k, o) Annotates a vertex or edge with object o indexed by key k.
getAnnotation(Object k) Returns the object indexed by k annotating a vertex or edge.
removeAnnotation(Object k) Removes the annotation on a vertex or edge indexed by k and returns it.
There are various methods for changing the direction of edges. I think the only one we will need is:
reverseDirection(e)
Reverse the direction of an edge.
Throws InvalidEdgeException if the edge is undirected
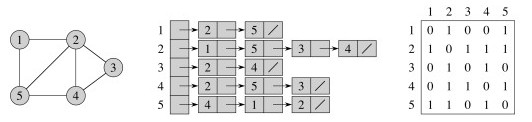
There are two classic representations: the adjacency list and the adjacency matrix.
In the adjacency list, vertices adjacent to vertex v are listed explicitly on linked list G.Adj[v] (assuming an array representation of list headers).
In the adjacency matrix, vertices adjacent to vertex v are indicated by nonzero entries in the row of the matrix indexed by v, in the columns for the adjacent vertices.
Adjacency List and Matrix representations of an undirected graph:
Adjacency List and Matrix representations of a directed graph:
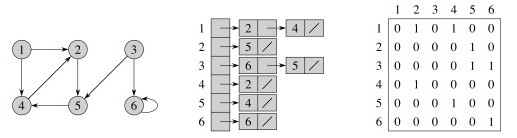
Please be sure you understand the above representations before reading on. Then answer the following questions.
Can you identify the asymptotic complexities of the following methods in each representation? You will be asked on quizzes and exams!!!
Are edges first class objects in the above representations? Where do you store edge information in the undirected graph representations?
Be sure you understand why the following Θ results are true.
So the matrix takes more space and more time to list adjacent matrices, but is faster to test adjacency of a pair of matrices.
Goodrich & Tamassia (reading in Laulima) propose a representation that combines an edge list, a vertex list, and an adjacency list for each vertex:
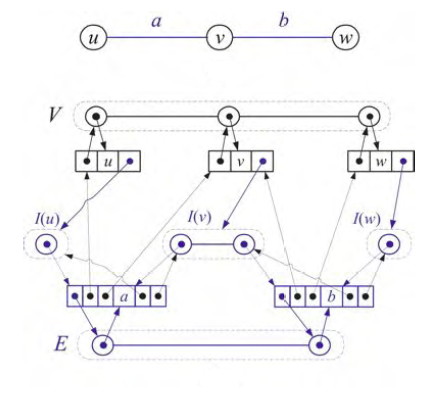
The sets V and E can be represented using a dictionary ADT. In many applications, it is especially important for V to enable fast access by key, and may be important to access in order. Each vertex object has an adjacency list I (I for incident), and the edges reference both the vertices they connect and the entries in this adjacency list. There's a lot of pointers to maintain, but this enables fast access in any direction you need, and for large sparse graphs the memory allocation is still less than for a matrix representation.
See also Newman (2010) chapter 9, posted in Laulima, for discussion of graph representations.
Before starting with Cormen et al.'s more complex presentation, let's discuss how BFS and DFS can be implemented with nearly the same algorithm, but using a queue for BFS and a stack for DFS. You should be comfortable with this relationship between BFS/queues and DFS/stacks.
Sketch of both algorithms:
Try starting with vertex q and run this using both a stack and a queue:
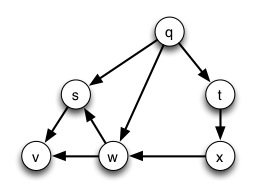

BFS's FIFO queue explores nodes at each distance before going to the next distance ("goes broad"). DFS's LIFO stack explores the more distant neighbors of a node before continuing with nodes at the same distance ("goes deep").
Search in a directed graph that is weakly but not strongly connected may not reach all vertices.
Specification: Given a graph G = (V, E) and a source vertex s ∈ V, output v.d, the shortest distance d (# edges) from s to v, for all v ∈ V. Also record v.π = u such that (u,v) is the last edge on a shortest path from s to v. (π stands for "parent". We can then trace the path back.)
Analogy Send a "tsunami" out from s that first reaches all vertices 1 edge from s, then from them all vertices 2 edges from s, etc. Like a tsunami, equidistant destinations are reached at the "same time".
The algorithm uses a FIFO queue Q to maintain the wavefront, such that v ∈ Q iff the tsunami has hit v but has not come out of it yet. WHITE vertices have not been encountered yet; GRAY vertices have been encountered but processing is still in progress (this prevents us from queuing a vertex more than once if it is reachable by different paths); and BLACK vertices are done being processed (everything reachable from them has been queued for exploration).
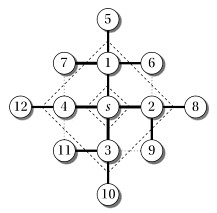

At any given time Q has vertices with d values i, i, ... i, i+1, i+1, ... i+1. That is, there are at most two distances on the queue, and values increase monotonically.
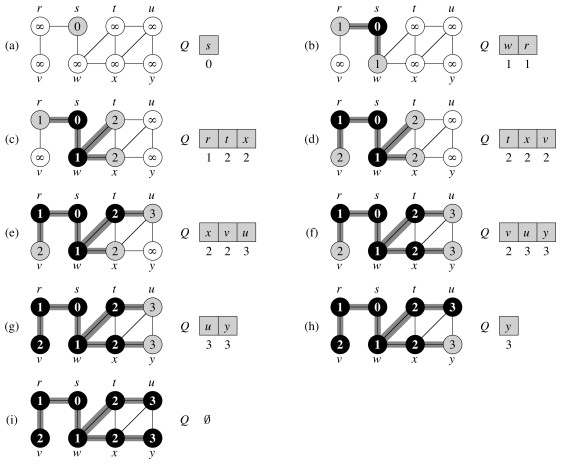
Let's do another example, starting at node s. (Number the nodes by their depth, then click to compare your answer):
(This is an aggregate analysis, a method covered in more detail in Topic 15.) Because the GRAY color prevents multiple queuing, every reachable vertex is enqueued once in line 17, for O(V). We examine edge (u, v) in line 12 only when u is dequeued, so every edge is examined at most once if directed and twice if undirected, for O(E). The rest is constant. Therefore, the total is O(V+ E).
The shortest distance δ(s, v) from s to v is the minimum number of edges across all paths from s to v, or ∞ if no such path exists.
A shortest path from s to v is a path of length δ(s, v).
It can be shown that BFS is guaranteed to find the shortest paths to all vertices from a start vertex s: v.d = δ(s, v), ∀ v at the conclusion of the algorithm. See the CLRS text for a tedious proof.
Informally, we can see that all vertices at distance 1 from s are enqueued first, then via them all nodes of distance 2 are reached and enqueued, etc., so inductively it would be a contradiction if BFS reached a vertex c by a longer path than the shortest path because the last vertex u on the shortest path to the given vertex v would have been enqueued first and then dequeued to reach v.
The predecessor subgraph of G is
Gπ = (Vπ, Eπ) where
Vπ = {v ∈ V : v.π ≠ NIL} ∪ {s} and
Eπ = {(v.π, v) : v ∈ Vπ − {s}}
A predecessor subgraph Gπ is a breadth-first tree if Vπ consists of exactly all vertices reachable from s and for all v in Vπ the subgraph Gπ contains unique simple and shortest paths from s to v.
BFS constructs π such that Gπ is a breadth-first tree.
The following material is covered on the second day.
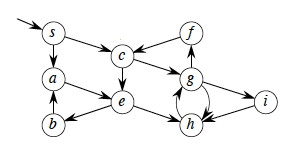
Given G = (V, E), directed or undirected, DFS explores the graph from every vertex (no source vertex is given), constructing a forest of trees and recording two time stamps on each vertex:
Time starts at 0 before the first vertex is visited, and is incremented by 1 for every discovery and finishing event (as explained below). These attributes will be used in other algorithms later on.
(The example figure shows only discovery times.)
Since each vertex is discovered once and finished once, discovery and finishing times are unique integers from 1 to 2|V|, and for all v, v.d < v.f.
(Some presentations of DFS pose it as a way to visit nodes, enabling a given method to be applied to the nodes with no output specified. Others present it as a way to construct a tree. The CLRS presentation is more complex but supports a variety of applications. It is worth the effort to understand the CLRS approach.)
DFS explores every edge and starts over from different vertices if necessary to reach them (unlike BFS, which may fail to reach subgraphs not connected to s).
As it progresses, every vertex has a color with semantics similar to BFS:
- WHITE = undiscovered
- GRAY = discovered, but not finished (still exploring vertices reachable from it)
- v.d records the moment at which v is discovered and colored gray.
- BLACK = finished (have found everything reachable from it)
- v.f records the moment at which v is finished and colored black.
DFS(G) 1 for each vertex u ∈ G.V 2 u.color = WHITE 3 u.π = NIL 4 time = 0 5 for each vertex u ∈ G.V 6 if u.color == WHITE // only explore from undiscovered vertices 7 DFS-VISIT(G, u) DFS-VISIT(G, u) 1 time = time + 1 // u has just been discovered: record time 2 u.d = time 3 u.color = GRAY // u is now on active path 4 for each v ∈ G.Adj[u] // explore edge (u,v) 5 if v.color == WHITE 6 v.π = u 7 DFS-VISIT(G, v) 8 u.color = BLACK // u finished: blacken and record finish time 9 time = time + 1 10 u.f = time
While BFS uses a queue, DFS operates in a stack-like manner (using the implicit recursion stack in the algorithm above).
Another major difference in the algorithms as presented here is that DFS will search from every vertex until all edges are explored, while BFS only searches from a designated start vertex.
One could start DFS with any arbitrary vertex, and continue at any remaining vertex after the first tree is constructed. Regularities in the book's examples (e.g., processing vertices in alphabetical order, or always starting at the top of the diagram) do not reflect a requirement of the algorithm.
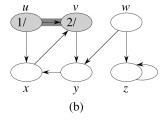
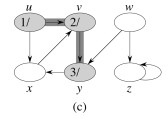
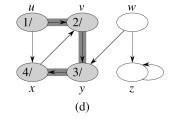
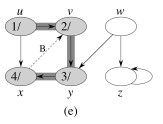
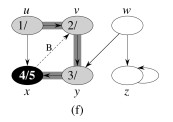
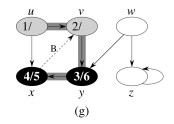
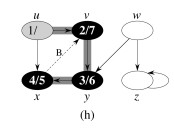
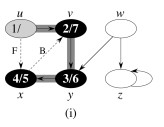
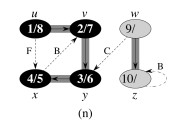
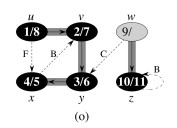
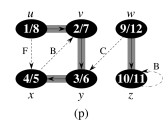
Let's do this example: start with the upper left node, label the nodes with their d and f, then click to compare your answer:
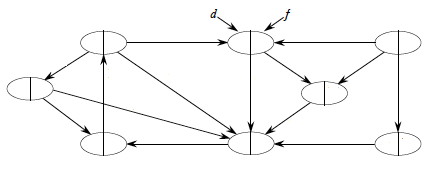

The analysis uses aggregate analysis (Topic 15), and is similar to the BFS analysis, except that DFS is guaranteed to visit every vertex and edge, so it is Θ not O:
Θ(V) to visit all vertices in lines 1 and 5 of DFS;
Σv∈V |Adj(v)| = Θ(E) to process the adjacency lists in line 4 of DFS-Visit.Aggregate analysis: we are not attempting to count how many times the loop of line 4 executes each time it is encountered, as we don't know |Adj(v)|. Instead, we sum the number of passes through the loop in total: all edges will be processed. When it's hard to count one way, think of an easier way to count!The rest is constant time.
Therefore, the total time complexity is Θ(V + E).
This classification will be useful in forthcoming proofs and algorithms.
Here's a graph with edges classified, and redrawn to better see the structural roles of the different kinds of edges (the shaded edges are tree edges):
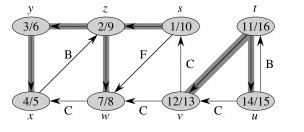
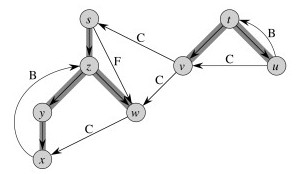
These theorems show important properties of DFS that will be used later to show how DFS exposes properties of the graph.
After any DFS of a graph G, for any two vertices u and v in G, exactly one of the following conditions holds:
- The intervals [u.d, u.f] and [v.d, v.f] are entirely disjoint, and neither u nor v is a descendant of the other in the DFS forest.
- The interval [u.d, u.f] is contained entirely within the interval [v.d, v.f], and u is a descendant of v in a DFS tree.
- The interval [v.d, v.f] is contained entirely within the interval [u.d, u.f], and v is a descendant of u in a DFS tree.
The Theorem essentially states that the d and f visit times are well nested, like nested parentheses. See the CLRS text for proof. For example, the left hand graphic below shows this nesting for the graph and discovery/finish times shown:
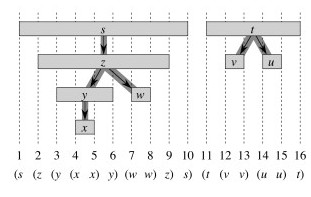

Vertex v is a proper descendent of vertex u in the DFS forest of a graph iff u.d < v.d < v.f < u.f. (Follows immediately from parentheses theorem.)
Also, (u, v) is a back edge iff v.d ≤ u.d < u.f ≤ v.f; and a cross edge iff v.d < v.f < u.d < u.f.
Vertex v is a descendant of u iff at time u.d there is a path from u to v consisting of only white vertices (except for u, which was just colored gray).
(Proof in textbook uses v.d and v.f. Metaphorically and due to its depth-first nature, if a search encounters an unexplored location, all the unexplored territory reachable from this location will be reached before another search gets there.)
Recall that DFS can be run on undirected graphs as well. The DFS theorem states:
DFS of an undirected graph produces only tree and back edges: never forward or cross edges.
(Proof in textbook uses v.d and v.f. Informally, this is because the edges being bidirectional, we would have traversed the supposed forward or cross edge earlier as a tree or back edge.)
A directed acyclic graph (DAG) is a good model for processes and structures that have partial orders: You may know that a > c and b > c but may not have information on how a and b compare to each other.
One can always make a total order out of a partial order. This is what topological sort does. A topological sort of a DAG is a linear ordering of vertices such that if (u, v) ∈ E then u appears somewhere before v in the ordering.

Topological-Sort(G) is actually a modification of DFS(G) in which each vertex v is inserted onto the front of a linked list as soon as finishing time v.f is known.
Some real world examples include
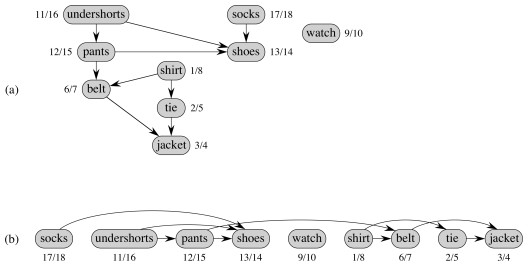
Here is the book's example ... a hypothetical professor (not me!) getting dressed. Part (a) shows the original search, and (b) the resulting topological sort (ordered by finish time, showing what the professor should put on first). On what vertex did the search start? If the search started at another vertex, would it work? Would the results be the same?
We can make it a bit more complex, with a hockey goalie's outfit. Run Topological-Sort and click to compare your answer:
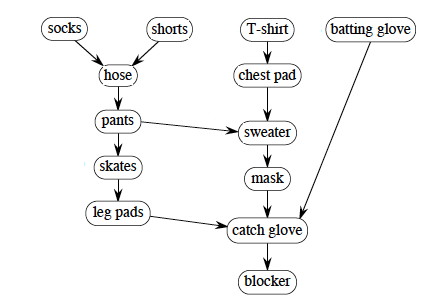
The answer given starts with the batting glove and works left across the unvisted nodes. What if we had started the search with socks and worked right across the top nodes? If you put your clothes on differently, how could you get the desired result? Hint: add an edge.
One could start with any vertex, and once the first tree was constructed continue with any artibrary remaining vertex. It is not necessary to start at the vertices at the top of the diagram. Do you see why?

Time complexity is Θ(V + E) since DFS complexity dominates this simple algorithm.
Lemma: A directed graph G is acyclic iff a DFS of G yields no back edges.
See text for proof, but it's quite intuitive:
⇒ (if) A back edge by definition is returning to where one started, which means it completes a cycle.
⇐ (only if) When exploring a cycle the last edge explored will be a return to the vertex by which the cycle was entered, and hence classified a back edge.
Theorem: If G is a DAG then Topological-Sort(G) correctly produces a topological sort of G.
It sufficies to show that
if (u, v) ∈ E then v.f < u.f
because then the linked list ordering by f will respect the graph topology.
When we explore (u, v), what are the colors of u and v?
Given a directed graph G = (V, E), a strongly connected component (SCC) of G is a maximal set of vertices C ⊆ V such that for all u, v ∈ C, there is a path both from u to v and from v to u.
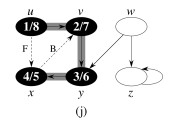
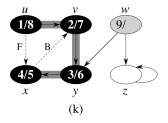
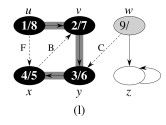
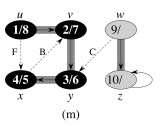
What are the Strongly Connected Components? (Click to see.)
The algorithm uses GT= (V, ET), the transpose of G = (V, E). GT is G with all the edges reversed.
Strongly-Connected-Components (G)
1. Call DFS(G) to compute finishing times u.f for each vertex u ∈ E.
2. Compute GT
3. Call modified DFS(GT) that considers vertices
in order of decreasing u.f from line 1.
4. Output the vertices of each tree in the depth-first forest
formed in line 3 as a separate strongly connected component.
Suppose that DFS starts at vertex c, and then from vertex b.
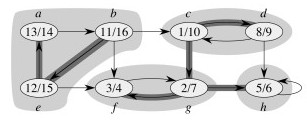
Now, in the transpose graph, DFS starts on vertex b, because it has the highest finish time 16, and then on c (finish time 10), and g.
(This explanation differs from the book's formal proof.)
G and GT have the same SCC. Proof:
A DFS from any vertex v in a SCC C will reach all vertices in C (by definition of SCC).
So how does the second search on GT help avoid inadvertent inclusion of v' in C?
In the example above, notice how node c corresponds to v and g to v' in the argument above. But we need to also say why nodes like b will never be reached from c in the second search. It is because b finished later in the first search, so was processed earlier and already "consumed" by the correct SCC in the second search, before the search from c could reach it. The following fact is useful in understanding why this would be the case.
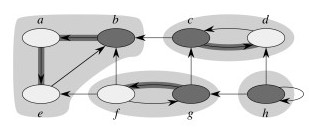
Here is GSCC for the above example:
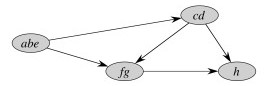
The first pass of the SCC algorithm essentially does a topological sort of the graph GSCC (by doing a topological sort of constituent vertices). The second pass visits the components of GTSCC in topologically sorted order such that each component is searched before any component that can reach that component.
Thus, for example, the component abe is processed first in the second search, and since this second search is of GT (reverse the arrows above) one can't get to cd from abe. When cd is subsequently searched, one can get to abe but it's vertices have already been visited so can't be incorrectly included in cd.
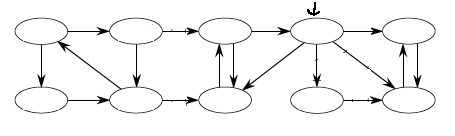
Start at the node indicated by the arrow; simulate a run of SCC on it; then click to compare your answer:
We have provided an informal justification of correctness: please see the CLRS book for a formal proof of correctness for the SCC algorithm. Here we consider time complexity.

The CLRS text says we can create GT in Θ(V + E) time using adjacency lists.
The SCC algorithm also has two calls to DFS, and these are Θ(V + E) each.
All other work is constant, so the overall time complexity is Θ(V + E).
An articulation point or cut vertex is a vertex that when removed causes a (strongly) connected component to break into two components.
A bridge is an edge that when removed causes a (strongly) connected component to break into two components.
A biconnected component is a maximal set of edges such that any two edges in the set lie on a common simple cycle. This means that there is no bridge (at least two edges must be removed to disconnect it). This concept is of interest for network robustness.
Graph or Network analysis is of considerable importance in understanding biological, information, social, and technological systems; and there are many other graph concepts and analytic methods. See the Newman (2010) chapters for more, or enroll in ICS 422 Network Science Methodology or ICS 622 Network Science.
We take a brief diversion from graphs to introduce amortized analysis and efficient processing of union and find operations on sets, both of which will be used in subsequent work on graphs. Then we return to graphs with concepts of minimum spanning trees, shortest paths, and flows in networks.